مقدمة في الجبر الخطي
مقدمة
الجبر الخطي هو من أهم فروع الرياضيات , وهو فرع من الرياضيات البحتة وفرع من علم الجبر الأساسي ويتناول الجبر الخطي موضوعات متعددة مثل الفضاءات المتجهية والأنظمة الخطية والمصفوفات وإلخ…
مفهوم الجبر
الجبر هو فرع الرياضيات الذي يستبدل الأرقام بالحروف والرموز ذات الدلالات , والجبر الخطي هو من أهم فروع علم الجبر حيث يتناول مواضيع الجبر في أنظمة خطية.
خطة الجبر الخطي
Systems of Linear equations / أنظمة المعادلات الخطية
Matrices and Determinates / المصفوفات والمحددات
Operations of matrices / العمليات على المصفوفات
Points and Vectors / النقاط والمتجهات
2D and 3D / ثنائي الأبعاد وثلاثي الأبعاد
Introduction to NumPy / مقدمة لمكتبة نمباي الأساسية في بايثون
معادلات جبرية
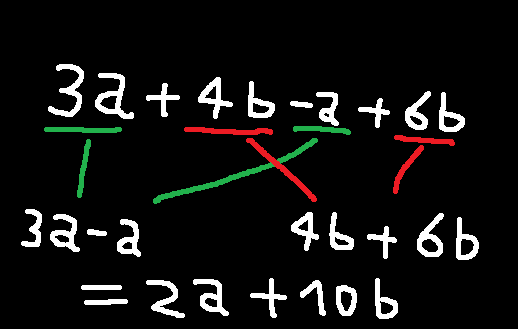
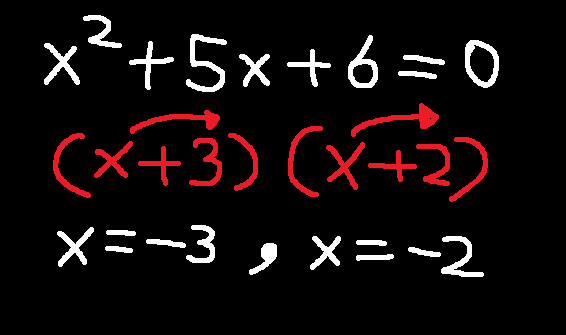
التمثيل البياني للنقاط
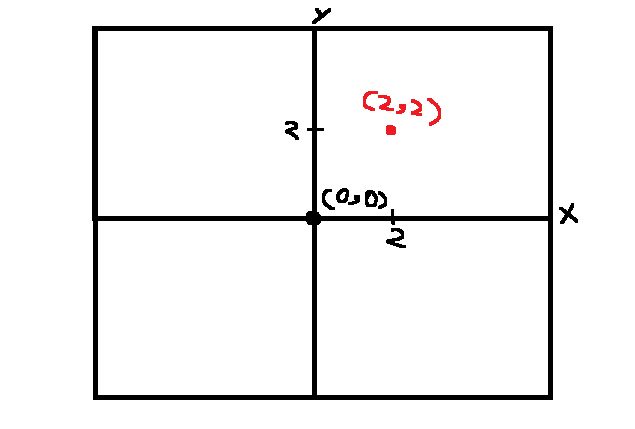
لنفترض أنه لدينا نقطة (2,2) في تمثيل بياني ثلاثي الأبعاد فسيكون بهذا الشكل :
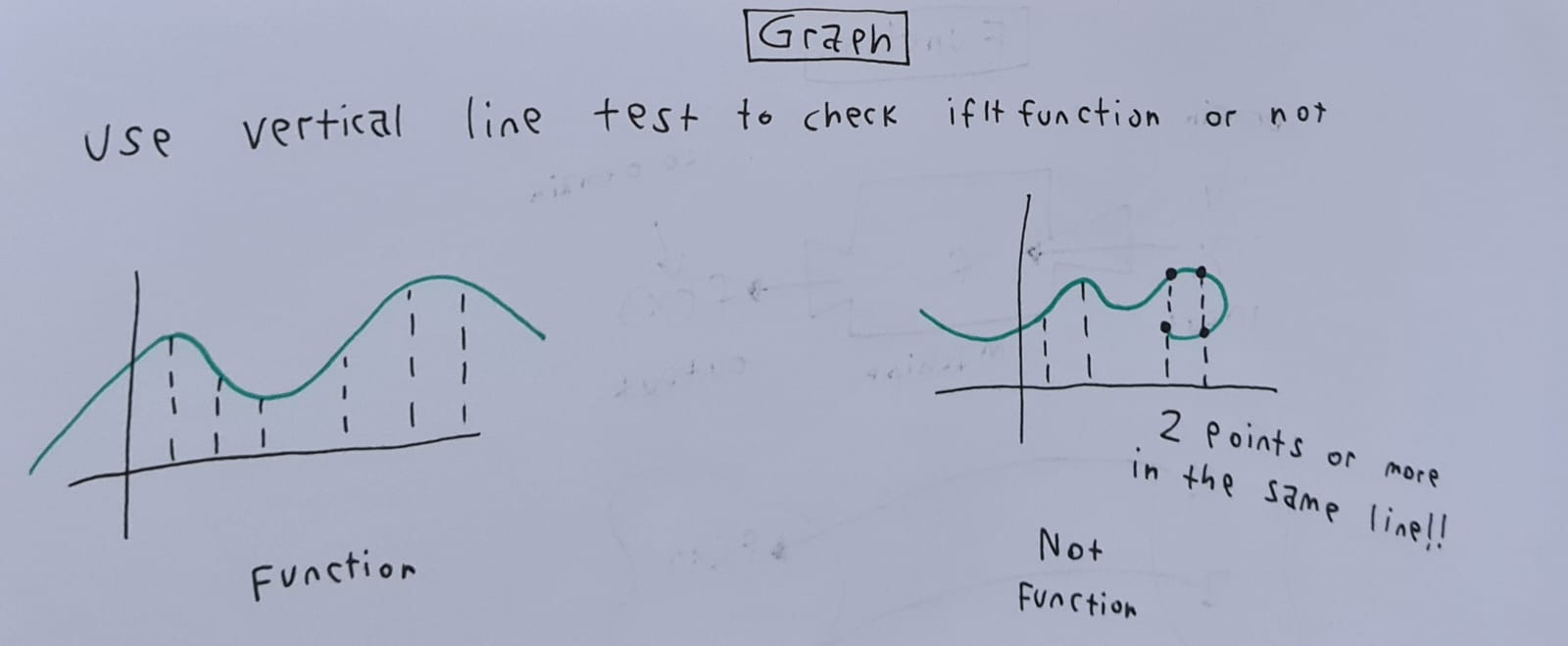
وهذا تمثيل الدوال في طريقة الرسم البياني
راجع من هنا درس ماقبل التفاضل والتكامل الرابط
ولكن ليس من الدائم أن يكون الرسم البياني عبارة عن محورين فقط أو في عالم ثنائي الأبعاد
تمثيل بياني ثلاثي الأبعاد
وهو التمثيل الواقعي الذي يمثل حياتنا اليومية على 3 أبعاد :
- الطول
- العرض
- الإرتفاع
وغالباً مايضيف الفيزيائيين بعداً رابعاً وهو : 4. الزمن لكنه ليس محور حديثنا ولايهمنا كثيراً .

وتمثيل النقاط غالباً يكون نفس ماهو لكن مع إضافة بعد ثالث يؤثر قليلاً
المتجهات / Vectors
هو عنصر مثل السهم بين نقطتين وغالبا مايكون من نقطة الصفر تجاه نقطة أخرى
من المتجه يمكن حساب طوله وحساب وحدة المتجه
طول المتجه = جذر كل عناصر المتجه مع تربيع كل عنصر وجمعها مع بعضها البعض
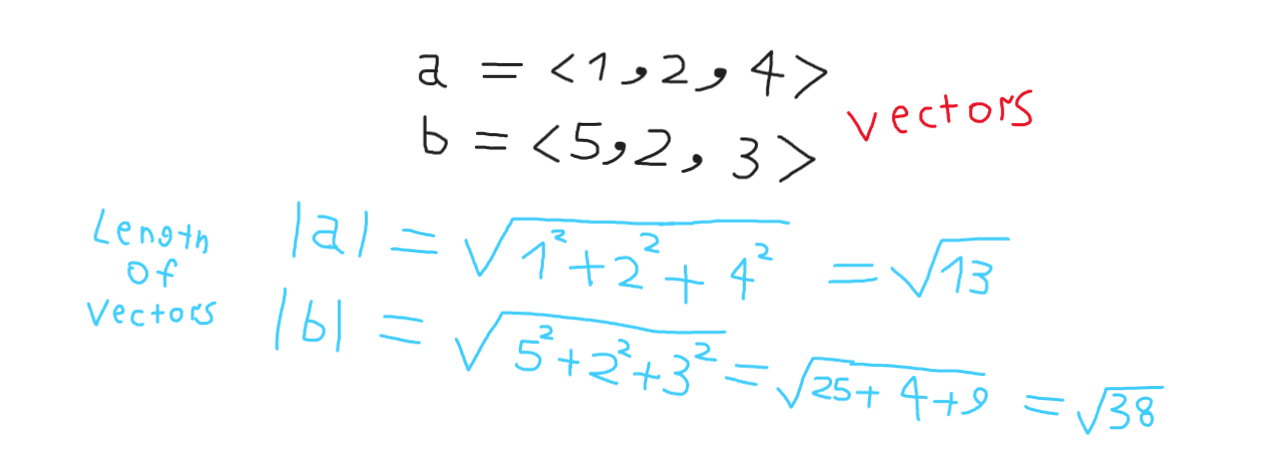
ويمكن بعد ذلك إيجاد وحدة المتجه أو ماتسمى :
Unit vector
وهو المتجه نفسه على طوله , حيث كل عنصر في المتجه ينقسم على طول المتجه كاملاً
Matrices / المصفوفات
وهي محور حديثنا في الأساس , المصفوفة هي مجموعة أرقام داخل مكان معين ذو خصائص محددة.
يمكن من المصفوفات إيجاد :
- محدد المصفوفة
وذلك عن طريق الضرب القطري لكل عناصر المجموعة ثم الطرح وهو طريقة يطول شرحها
جمع مصفوفتين
ضرب مصفوفتين
طرح بين مصفوفتين
قسمة مصفوفة على مصفوفة
والمصفوفات التي نقصدها هي الـ :
Matrix
وهي المصفوفات ثنائية الأبعاد حصراً دون المصفوفات أحادية الأبعاد أو ثلاثية الأبعاد , راجع ذلك في كتابي برمجة المصفوفات
ومعرفة المصفوفات تحديداً مهمة قبل الدخول في تعلم مكتبة نمباي الرياضية في لغة بايثون , ونستخدم نمباي لإجراء حسابات رياضية جبرية معقدة ومن ضمنها تعديل إعدادات نماذج تعلم الآلة ووظائف أخرى .
مصادر ومراجع :
- ويكيبيديا - جبر خطي
- Calculus Book - For Dummies By Mark Ryan
- Pre Algebra Book - For Dummies
- Freecodecamp - Precalculus
- Imperial college of London - Mathematics for Machine Learning: Linear Algebra on Coursera
- Deeplearning.ai - Linear Algebra for Machine Learning and Data Science on Coursera